Modeling Varying Iridescence on Microfacet Models

A Practical Extension to Microfacet Theory
for the Modeling of Varying Iridescence

Laurent Belcour	Pascal Barla

Motivation

Birth of this Research Project

Classical microfacets

Iridescent microfacets

It all started with a blog post
We wanted to achieve it real-time
- First guess: "should be easy"
- Took us 8 months ...

Maxwell Render blog

Before getting further, I would like to by share some thoughts on how we came to work on such topic. *click*

It all started about a year ago when I discovered a blog post from the Maxwell render team. Pascal and I were already discussing how it was possible to extend the range of appearance in CG and we were impressed by the visual impact of adding a iridescence to surfaces. *click* It is really that blog post that made us start this research project and I would like to pay a tribute to them. This blog post had more impact on us that any of the papers we read on the subject. *click*

Now while reading this blog post we both thought that it would be easy to do a real-time portage of this spectral model and that it wasn't worth any publication at all. *click*

However, what I will tell you today is how this apparently simple portage resolved into something much more complex.

Goniochromism

Thin-Film Reflectance

Thin-Film Interference: Using Phase

$\eta_{1}$

$\eta_{2}$

$\vec{\eta}_{3}$

$\mathcal{D}$

$\mathcal{D}$ is called the Optical Path Difference

To understand how interference produces colors, we have to dive into wave optics and analyze the relative phase and amplitude of each outgoing light waves. I will illustrate how interference occurs and create colors in this example. In this case, we assume that the incoming light has a single wavelength.*click*

We will look at the waves corresponding to the blue and green light rays. Note that those waves have a different amplitude due to the transmission and reflection coeffcients. They also have a different shift which will have an important impact.*click*

When we sum those waves together, the difference in shift can cause destructive or constructive interference meaning that the amplitude of the black wave depends on both the amplitude of the green and blue wave but also their relative shift. Since the shift is wavelength dependant, the spectral response of this surface with be colored and create those rainbow pattern we just saw.*click*

This shift is caused by two things. The first one is the optical path difference denoted 'D' here. The optical path difference is the difference in distance between the two light paths from the gray dot to where they align with respect to the outgoing planar wave (the blue and green dot respectively). The second one is the reflection by the interfaces. Conductors and dielectric introduce a non negligeable change in phase that needs to be accounted when resolving interference. Our model is the first to correctly account for the polarized phase shift due to conductors and dielectrics. However in this talk I will simplify the discussion by phase shift into D and not talking about the different polarization plane.*click*

If we add more bounces we will have to account for the amplitude and phase of other light waves. However, it is to notice that the shift between waves will always be a mutliple of the one bounce shift.

Thin-Film Interference : Airy Summation

$\eta_{1}$

$\eta_{2}$

$\vec{\eta}_{3}$

outgoing reflectance $ R = |\vec{r}|^2$

with $\vec{r} = \color{red}{\vec{r}_{12}} + \color{blue}{t_{12}} \color{green}{\vec{r}_{23}e^{i \Delta\phi}} \color{orange}{t_{21}} + \cdots$

$$\vec{r} = \color{red}{\vec{r}_{12}} + \color{blue}{t_{12}} \color{green}{\dfrac{\vec{r}_{23}e^{i \Delta\phi}}{1 - \vec{r}_{21}\vec{r}_{23}e^{i \Delta\phi}}} \color{orange}{t_{21}}$$

Analytical form: Airy summation

Naive Implementation


RGB renderer - Naive implementation

Comparison with Spectral Renderer



RGB renderer - Naive implementation	128 spectral samples - Naive implementation

Issue: Spectral Aliasing

Using Naive RGB rendering does spectral aliasing
- Affect goniochromatic materials
- Can be solved using spectral rendering
Spectral rendering is not an option for video-games
- Can't tabulate the range of all parameters as [Smits and Meyer 1992]
Our solution: spectral antialiasing
- Account for spectral integration inside the model
- Required a novel view on Airy's summation

In signal processing, an insufficent sampling of a function causes aliasing and this is exactly what we see here. This is due to the use of only one spectral sample per channel and *click* of course the use of a spectral renderer will solve this issue.*click*

However we were trying to implement such appearance for real-time RGB scenario and spectral integration wasn't possible. *click*. Another issue we had to face is that to be able to use both conductors and dielectric as the bottom interface, we could not precompute the spectral integral and store it in a look-up table. There was too many dimensions to correctly fit it in memory.*click*

So we developped a method that enables to perform spectral antialiasing on the fly by directly incorporating spectral integration into the reflectance term. This required us to develop a novel view on Airy's summation that was new even to optics community.

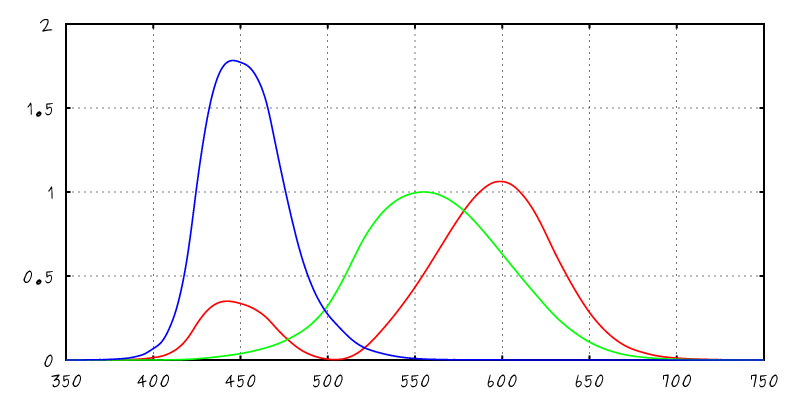
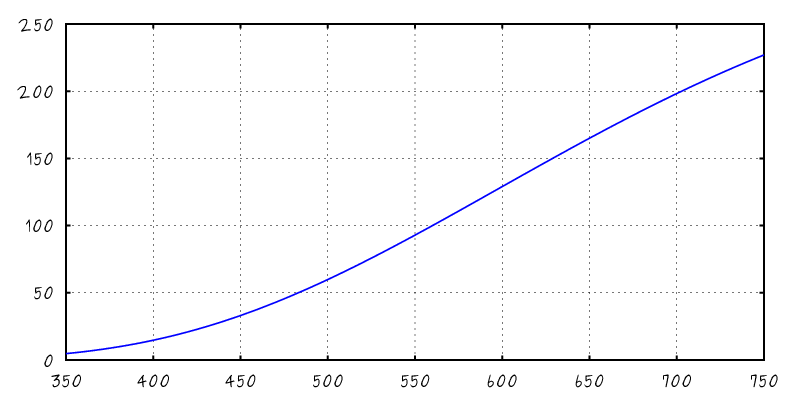
Spectral Integration with Sensor Sensitivity

$$\int$$

$$\times$$

$$\mbox{d}\lambda$$


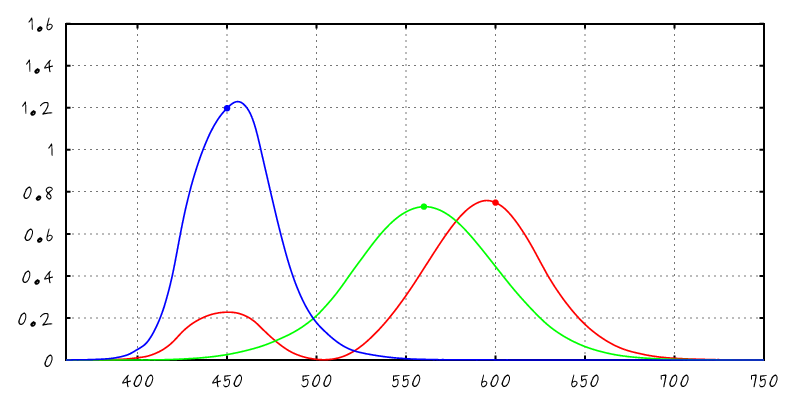
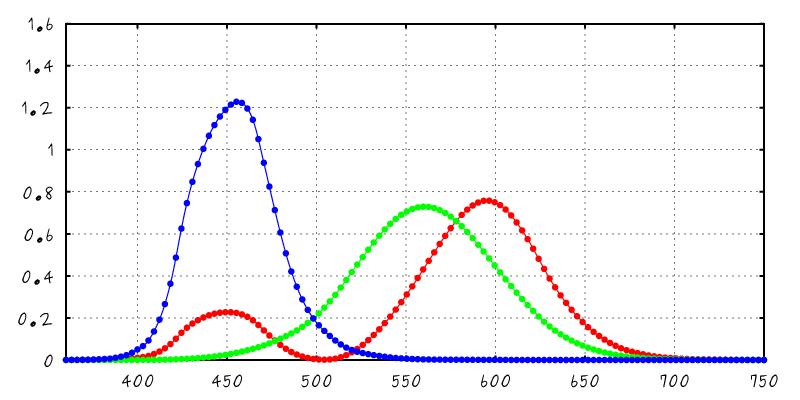
XYZ Color Matching Curves	Spectral BRDF	Illuminant A

Our Solution: Pre-Integration

Under approximations
- Illuminant constant per sensitivity function
- Material properties (IORs) constant as well
We can approximate the spectral integral in closed-form

$$R \! = \! \int \hspace{500px} \mbox{d}\lambda$$

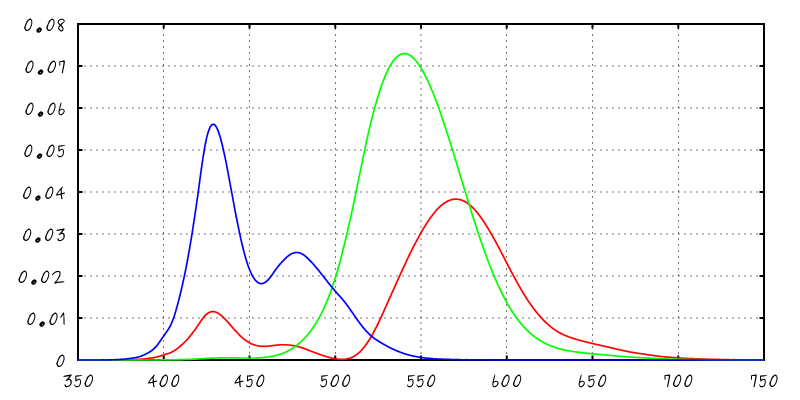XYZ times Reflectance

Airy Summation Reordered

Start from Airy summation

$$ \vec{r} = \color{red}{\vec{r}_{12}} + \color{blue}{t_{12}} \color{green}{\vec{r}_{23}e^{i \Delta\phi}} \color{orange}{t_{21}} + \cdots $$

Work on reflectivity and expand summation

$$R = |\vec{r}|^2 = C_0 + \sum_{m = 1}^{+\infty} C_m \color{blue}{\underbrace{\color{black}{\cos(m \Phi)}}}$$

equal phase difference

Airy Summation Reordered

Change of Variable

Express $R$ with respect to light frequency and not wavelength


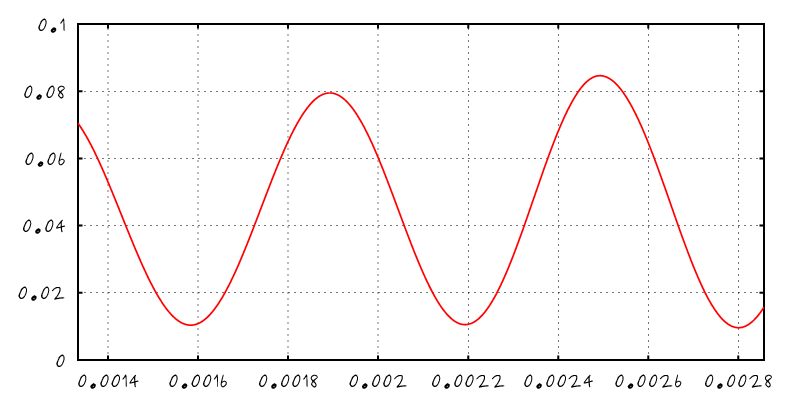$R(\lambda)$	$R(\mu)$ with $\mu \sim \frac{1}{\lambda}$

Fourier Transform of the Reflectance

Has discrete form with respect to light frequency


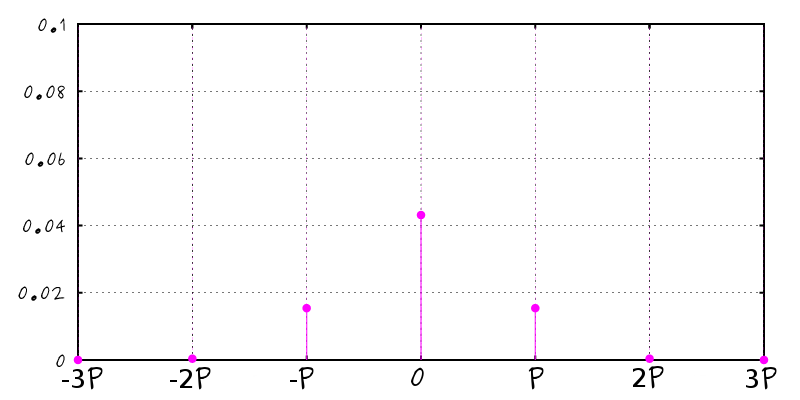$R(\mu)$ with $\mu \sim \frac{1}{\lambda}$	$\mathcal{F}\left[R\right]$

Integration in Fourier's Space

Using Parseval's theorem

$$R_j = \int \hat{R}(\mu) \, \overline{\hat{S}_j(\mu)} \, \mbox{d}\mu$$


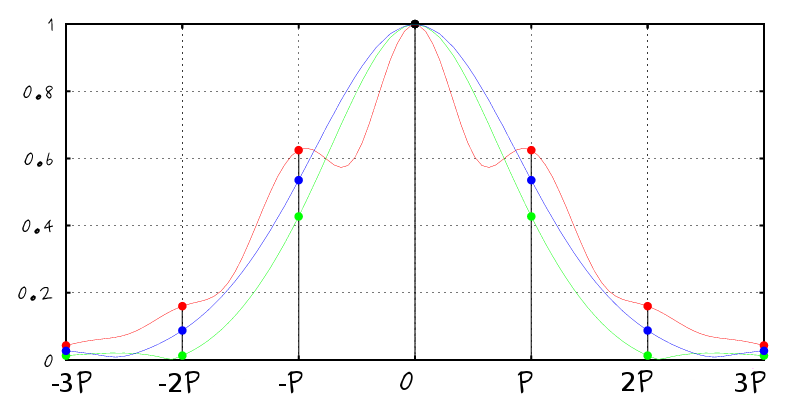Continuous integral		Discrete sum

$$\int$$

$$=$$

$$\sum$$

Integration in Fourier's Space

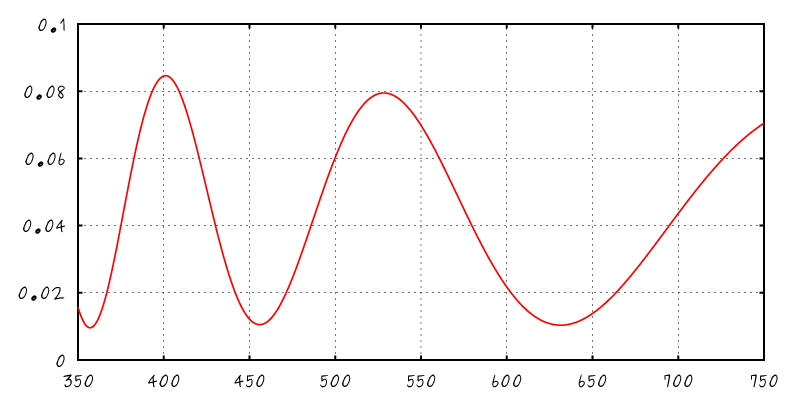
Evaluation of the sensitivity's Fourier Transform
- Can be precomputed as a RGB texture
- Can be approximated using 4 Gaussians

Real and imaginary table

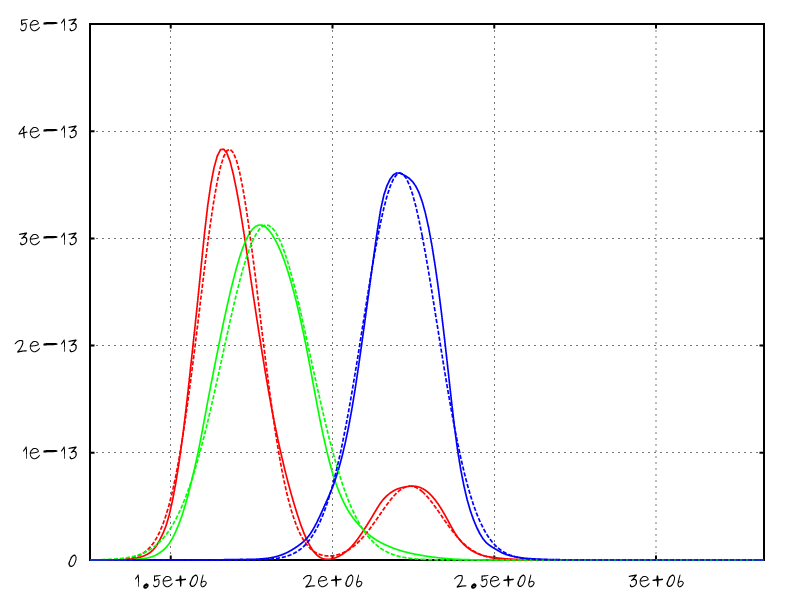
Fitting sensitivity functions with Gaussians

Integration in Microfacet Models

$$\rho = \frac{D(\mathbf{h}) \; G(\pmb{\omega}_i, \pmb{\omega}_o) \; F(\mathbf{h} \cdot \pmb{\omega}_i)}{4 \; (\pmb{\omega}_i \cdot \mathbf{n}) \; (\pmb{\omega}_o \cdot \mathbf{n})} $$

$$\rho = \frac{D(\mathbf{h}) \; G(\pmb{\omega}_i, \pmb{\omega}_o) \color{red}{R_i(\mathbf{h} \cdot \pmb{\omega}_i)}}{4 \; (\pmb{\omega}_i \cdot \mathbf{n}) \; (\pmb{\omega}_o \cdot \mathbf{n})} $$

Real-Time Rendering Constraints

Approximation for IBL and Area-Lights
- Decorrelate $R_i$ from the IBL/AL pre-integration
- Evaluate $R_i$ using the mirror direction
- Oversaturate colors for rough materials

Results: Matlab Validation

Dielectric film over a dielectric base
Truncating the infinite sum
- Using up to 3 terms in the series
- In practice: still good up to 2

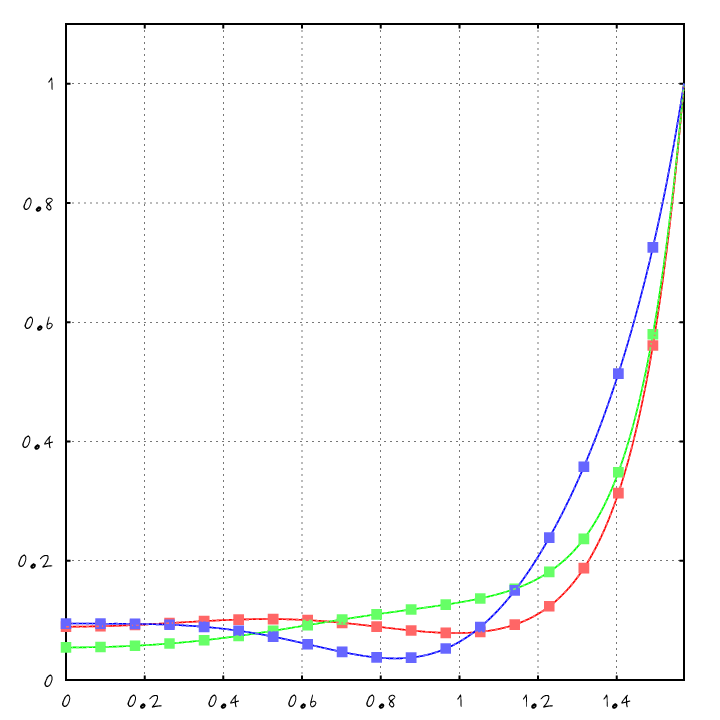
XYZ Reflectance w/r to Elevation

Results: Matlab Validation

Dielectric film over a dielectric base
Truncating the infinite sum
- Using up to 3 Optical Path Difference ($\mathcal{D}$)
- In practice: still good up to 2 $\mathcal{D}$
Also visible in Chromaticity Space
- Display curves w/r $[x,y] = \left[\frac{X}{X+Y+Z}, \frac{Y}{X+Y+Z}\right]$
- Our model faithfully reproduce the GT
Comparison with Naive RGB
- Fails to correctly reproduce color
- Often goes out of gamut

Chromaticity space x/y

Results: Offline Validation

Rendering in Mitsuba
- Conductor base with $\eta = 1.9$ and $\kappa = 1.5$
- Film of thickness $h = 550 \mbox{nm}$

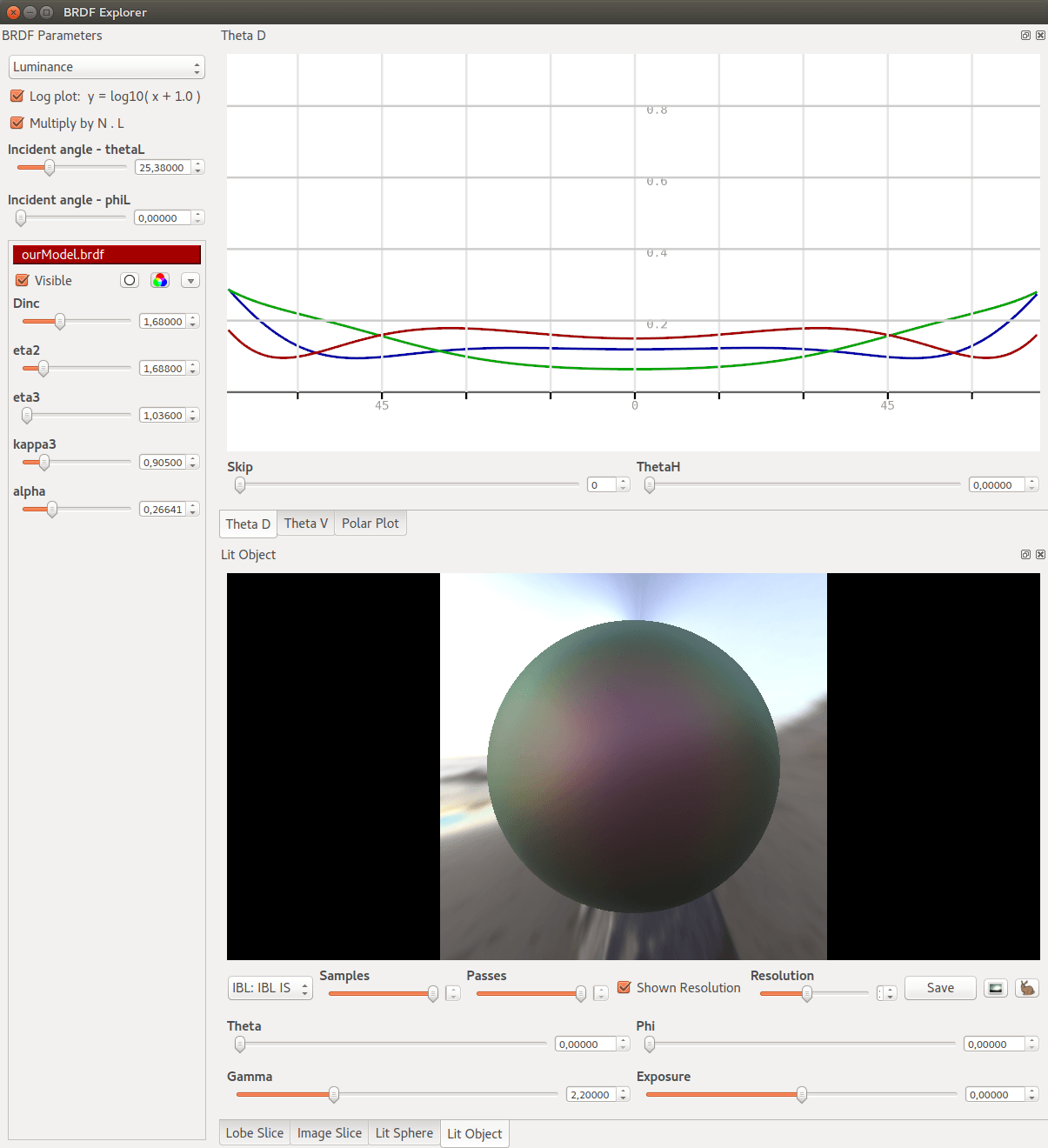
Ours (RGB) Ref. (Spectral) [Smits and Meyer 1992]

Results: Real-Time Validation

Rendering in BRDF Explorer, Gratin and Unity
- GLSL implementation provided in supp. mat.
- Using the Gaussian approximation of XYZ
Spatial Variations
- All parameters can be mapped to textures
- In practice: better vary only the thickness

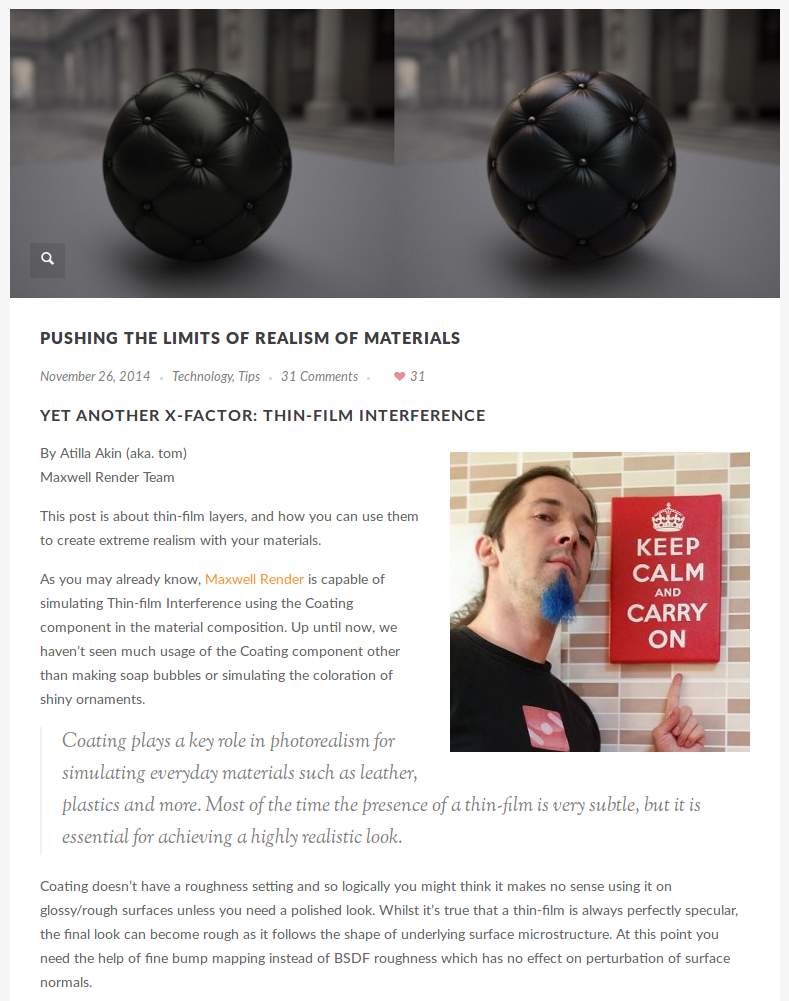
Results: Chair

Following Maxwell Render team's blog post
- Start from a classical microfacet model and add iridescence
- Similar appearance with same inputs
- Produce a subtle but convincing effect
Rendered in Mitsuba

Results: Robot Bust

Illustrate some possible appearances
- Increase thickness gradually
- Add texture to modulate thickness
Rendered in Mitsuba

Results: Beetle

Replicating special effect car paint
- Inside Unity's Scriptable RenderLoop
- Recorded on a Geforce 1080

Limitations

Varying Index of Refraction (IOR)
- Using measured data
- Fail to correctly replicated color for highly varying IORs

Glass base Mercury base Copper base

Summary

A extension to microfacet models
- Adding interference from thin-films
- Enable a richer set of appearances
Our contributions
- Spectral antialiasing from modified Airy summation
- Compatible with RGB real-time constraints
- Compatible with LOD rendering (see paper!)

Thank you for your attention


paper	supp. mat.	code

available at labs.unity.com

A Practical Extension to Microfacet Theory for the Modeling of Varying Iridescence

Motivation

Birth of this Research Project

Goniochromism

Thin-Film Reflectance

Thin-Film Interference: Using Phase

Thin-Film Interference : Airy Summation

Naive Implementation

Comparison with Spectral Renderer

Issue: Spectral Aliasing

Spectral Integration with Sensor Sensitivity

Our Solution: Pre-Integration

Airy Summation Reordered

Airy Summation Reordered

Airy Summation Reordered

Airy Summation Reordered

Change of Variable

Fourier Transform of the Reflectance

Integration in Fourier's Space

Integration in Fourier's Space

Integration in Microfacet Models

Real-Time Rendering Constraints

Results: Matlab Validation

Results: Matlab Validation

Results: Offline Validation

Results: Real-Time Validation

Results: Chair

Results: Robot Bust

Results: Beetle

Limitations

Summary

Thank you for your attention

A Practical Extension to Microfacet Theory
for the Modeling of Varying Iridescence