A Low-Discrepancy Sampler that Distributes Monte Carlo Errors
as a Blue Noise in Screen Space

Eric Heitz

Laurent Belcour

Unity Technologies

Victor Ostromoukhov

David Coeurjolly

Jean-Claude Iehl

Universite Lyon I

LittlestTokyo - 1 spp

LittlestTokyo - 2 spp

LittlestTokyo - 3 spp

LittlestTokyo - 4 spp

Random scrambling

3D model by Glen Fox

A screen-space sampler ?
🤨

LittlestTokyo - 4 spp

Random scrambling

Correlated scrambling

⚠ not practical

Correlated scrambling

⚠ not practical

Random scrambling

Let's look at the example of this rendered animation. Here, I randomly selected a different sampling sequences to compute the light transport integral in each pixel. I did that without any account for neighboring pixels.

*click* But, what we can do instead is to correlate the random sequences in neighboring pixels so that when one pixel has a high error, the next pixel has a low error. While this image is also rendered at four samples per pixels, we optimized it making sure that two consecutive pixels had different noise level. What we have here is not the method I am going to present, but a kind of reference that illustrates well what we want to acheive.

*click* Looking at both renderings side-by-side, maybe you see that the new rendering is more converged. Well, it isn't! The magnitude of the error between those images is almost unchanged. *click* Let's have a look at what changed.

Inset

LittlestTokyo - 4 spp

Random scrambling

Correlated scrambling

⚠ not practical

Power Spectrum

Our goal

Distributes error as a blue-noise in screen-space
- Reduces the visual error
- Reduces the error after denoising
State-of-the-art sampler
- Compatible with Owen scrambling [Owen 1998]
- Compatible with pmj02 [Christensen et al. 2018]
Lean & efficient
- Take two textures as input
- Additional cost : two fetches & XORs

Inset

Power Spectrum

LittlestTokyo - 4 spp + Denoising

Random scrambling

Correlated scrambling

⚠ not practical

Here is what happens when we apply a cross-bilateral denoiser on the correlated sampler. Denoisers are low pass filters that remove high frequency noise. But since this rendering's error has no energy in the low frequencies, most of the noise is cancelled.

*click* When we look at the random scrambled rendering, we see that a low frequency pattern persits after denoising. This is due to the low frequency part of the noise not being removed by the denoiser.

Because of that, the correlated scrambling once denoised has a lower error compared to random scrambling.

*click* This was a fundemental motivation for us. *click* So when we started this project, we defined that our goals were to achieve a blue-noise distribution of the error that would both reduce the perception of noise at low sample rates, but also reduce the error after denoising for higher sampler rate scenarios.

*click* We wanted to avoid any sacrifice regarding the convergence of individual pixels and worked with state-of-the-art sequences in mind such as Sobol with Owen scrambling or pmj02. *click* We also wanted to keep our method lean and efficient: as a result our new sampler only requires two low resolution textures as input and increase the cost of evaluating the sample by only two texture fetches and two xors.

Blue-Noise Dithered Sampling

Georgiev and Fajardo [2016]

Blue-Noise Dithered Sampling

Builds on research in Dithering
- Distribute quantization error
- Blue-noise is perceptually better
Extending dither masks
- nD dither mask
- using Simulated Annealing
Scramble sequences
- using Cranley-Patterson Rotations
- Offset sample $k$ with dither at pixel $i,j$ $$ \mu_{k,i,j} = \mbox{mod}\left(\epsilon_k + d_{i,j}\right) $$

Georgiev and Fajardo [2016]

Density

$$ d(i,j) $$

Random Dithering

$$ d(i,j) > \mbox{rand}(i,j) $$

Blue-Noise Dithering

$$ d(i,j) > bn(i,j) $$

$bn(i,j)$

1D Dither Mask

3D Dither Mask

They brought ideas from the dithering & half-toning litterature into Monte-Carlo rendering.

*click* One goal in this field is to quantize densities in perceptual pleasing way. If we want to quantize this image using only two pixel values, that are either zero or one. How can we maximize the perception of the input density ?

*click* One possible way is to randomly threeshold pixel values independently. The issue here is that we've lost some of the information about the image. For example, the background pattern.

*click* Now, we can use an blue-noise image to do the threesholding. Those blue-noise images are called dither masks. With this method, we obtain a much more pleasing result. For example, the background pattern is distinctible.

*click* In their work, Ilyian and Marcos extended the notion of dither mask to sampling. *click* While density threesholding only requires grayscale dither masks, sampling is defined in a higher dimensional space and *click* requires high dimensional dither masks. *click* And so, they generated those masks using simulated annealing ...

*click* and plugged their value in a fixed sequence using Cranley-Patterson rotations. CPR are simply a shift modulo one of samples in order to randomize them across pixels.

Blue-Noise Dithered Sampling

Problem solved ?

How to generate different sequences? ✗
How to distribute them in screen-space? ✗

If we put those concepts together, we obtain the following algorithm. To obtain the samples for the pixel highlighted here with BNDS, we fetch the dither mask and get a N dimensinonal vector. *click* In the unit hypercube, we shift modulo one the random numbers of the initial sequence and hit the rendering button.

*click* By doing so, BNDS makes the leap of faith that the blue-noise properties of the dither mask will be transfered into the rendering.

*click* And you could think that the problem is solved. BNDS seems to solve the two fundemental questions requires to our acheive blue-noise distribution that are: *click* how can generate many different sequences out of a single sequence. And *click* how do we distribute them in screen-space to acheive blue-noise distribution.

*click* Unfortunately, that doesn't work well. Or more precisely, that doesn't scale well. There are two main issues with this method that we are going to fix.

Issue #1 : CPR Considered Harmful

CPR : shifting samples

equivalent : shifting integrand

break stratification

Issue #1 : CPR Considered Harmful

Integrand

Numerical Integrand Error

Solution #1 : XOR Scrambling

Use a stratification preserving randomization
- XOR scrambling [Kollig and Keller 2002]
- Example with pmj02

pmj02 sequence

Preserve multi-stratification

first dim. XOR key: 1 0 1 1

Instead of using CPR, we choose to use a XOR scrambling because it preserves the convergence properties of (0,2)-sequences such as pmj02 or Sobol.

*click* Here is how it works for the first dimension of this pmj02 point set. *click* pmj02 ensure that only one point fall in each bin of those stratum.

*click* We iterate on the bits of a scrambling key and permut samples falling in the left and right nodes of a binary tree given the index in the scrambling key. *click* For example, we start with the first bit of the scrambling key and subdivide in two the unit space. *click* Since the bit is one, we permut the samples.

*click* We continue to the next bit and subdivide further and look for the bit's value. Here no change.

*click* Again, *click* here we do have to swap. *click* *click* Until we exhaust all the digits.

*click* The good thinkg about this scrambling scheme is that it preseves binary stratification. So if the input sequence is stratified, the scrambled sequence will be stratified as well. And this is what we can see with this scrambled pmj02 set.

XOR scrambling [Kollig & Keller 2002]

CPR [Georgiev and Fajardo 2016]

Chair - 8 spp

Issue #2 : Lack of Progressivity

Boxed - 1 spp

Georgiev and Fajardo [2016]

Power Spectrum of Error

Issue #2 : Lack of Progressivity

Boxed - 16 spp

Georgiev and Fajardo [2016]

Power Spectrum of Error

Issue #2 : Lack of Progressivity

Boxed - 16 spp

Georgiev and Fajardo [2016]

Power Spectrum of Error

White-noise as SPP increase

Solution #2 : Change the Optimization Space

Our Method : Test Integrands

Optimize with constant image-space integrands
- Same integrand for every pixel
- But different XOR keys per pixel

Scrambling mask

Integrand

& Samples

Resulting Image

Our idea was to design a family of rendering functions. We started with an ideal case, that is to have the same integrand for every pixel of the image.

*click* Say we wnat to integrate this 2D integrand.

*click* We use a scrambling mask that contains a different scrambling key in each pixel. *click* And we use it to scramble an input point set.

*click* Using a different sequence in each pixel to integrate the same integrand will produce a noise image here on the right. *click* *click*.

*click* Permuting the pixels in the scrambling mask is equivalent to do it in the noise image. We used simulated annealing like BNDS for it. Note that this optimization is done for a fixed sample count that we call the target sample count.

Our Method : Test Integrands

Optimize with constant image-space integrands
- Same integrand for every pixel
- But a different XOR key per pixel
Optimize using oriented Heavisides
- Random orientation $\theta$ and offset $d$
- Warning: $D$ dimensional integrands

Our Method : Test Integrands

Optimize with constant image-space integrands
- Same integrand for every pixel
- But a different XOR key per pixel
Optimize using oriented Heavisides
- Random orientation $\theta$ and offset $d$
- Warning: $D$ dimensional integrands
Robust to simple changes of integrand
- Varying orientation
- Varying smoothness
- Varying topology

Integrand	Integral - 1spp	Power Spectrum

Our Method : Sorting

Optimize every power of two spp
- Possible with (0,2)-sequences
- Sorting using XOR of sample index

However, optimizing for a specific sample count is good for final rendering but not for progressive rendering. So we rely on a second optmization stage to ensure that our sampler produces a blue-noise distribution of the error for every power of two sample count.

*click* We use the property that any power of two sub-sequence of a (0,2)-sequence is a (0,2)-sequence and applied a XOR on the index as an additional degree of freedom for our optimization.

*click* Let see how scrambling the index works on this pointset of eight samples. *click* We can list each point in this poinset according to its index from 0 to 7.

*click* We start by splitting the point set in two and look if using the first subset or the second subset achieve bluenoise at 4 samples per pixel. If the second subset is better, we permut the sample index. *click* We continue, with the 2 spp case by focusing on the first four points. *click* And we permut if necessary. *click* And again for the one spp case. *click* *click*.

Our Method : Sorting

Optimize every power of two spp
- Possible with (0,2)-sequences
- Sorting using XOR of sample index
Permits progressivity
- Blue-noise distribution across spp

Integrand	1spp	4spp	8spp	64spp	128spp

Summary

Scrambling mask

Sorting mask

function screen_space_sampler(i, j, index, dimension)
{
	// Fetch keys associated with pixel (i,j)
	scramble = scrambling_keys(i,j)
	sort = sorting_keys(i,j)

	// XOR the index
	index  = index ^ sort
	sample = sobol_owen(index, dimension)

	// XOR the sample
	sample = sample ^ scramble

	return sample
}

2 texture fetches + 2 XORs

QMC Integration

What can we do with two XORs ?

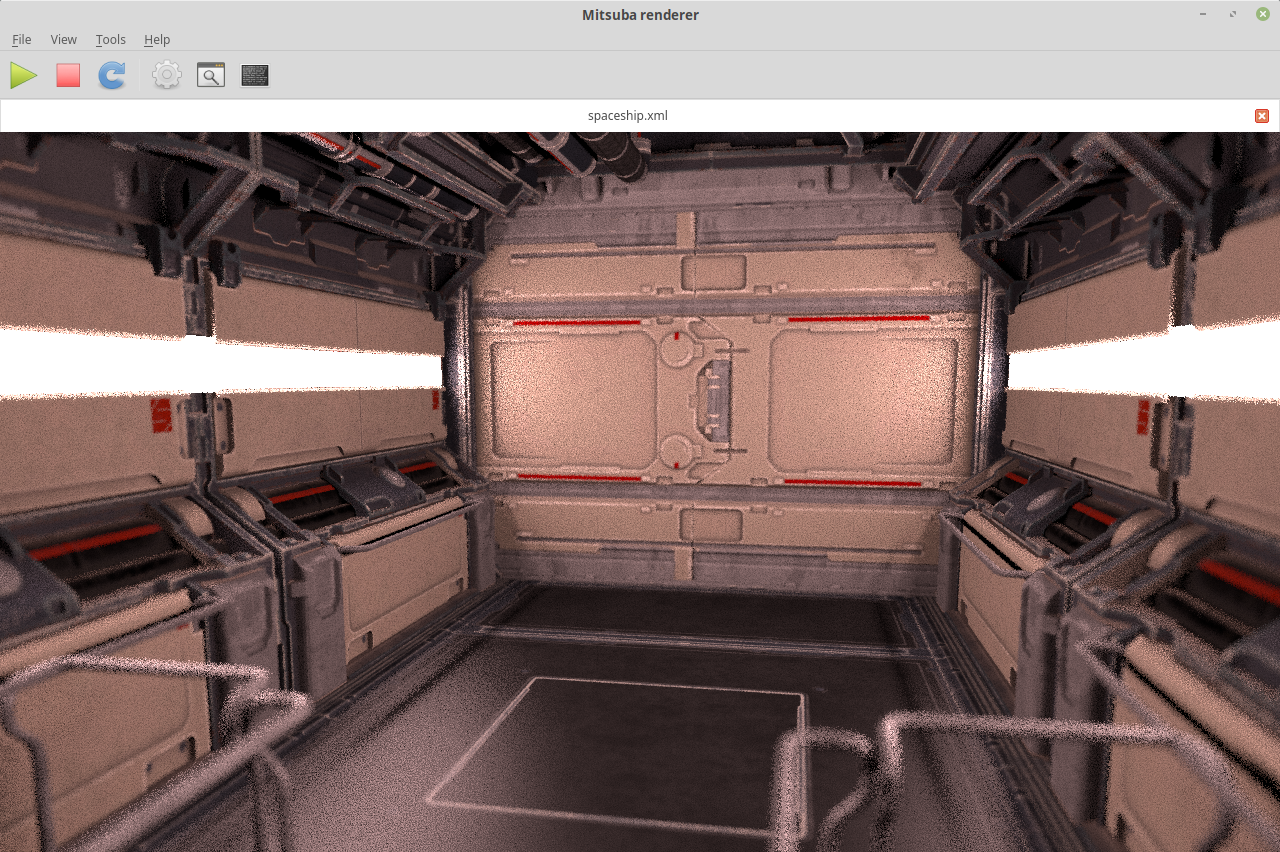
Results: Offline Rendering

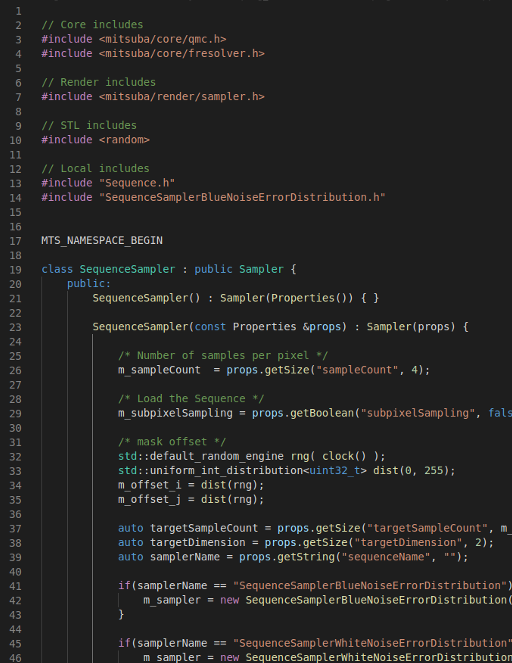
Direct Illumination in Mitsuba
- Implemented a new Sampler
- No impact on performances
Extensive study
- See our supplemental material
- Interactive HTML

Ours

Georgiev and Fajardo [2016]

Boxed - 1 spp

Ours

Georgiev and Fajardo [2016]

chair - 1 spp

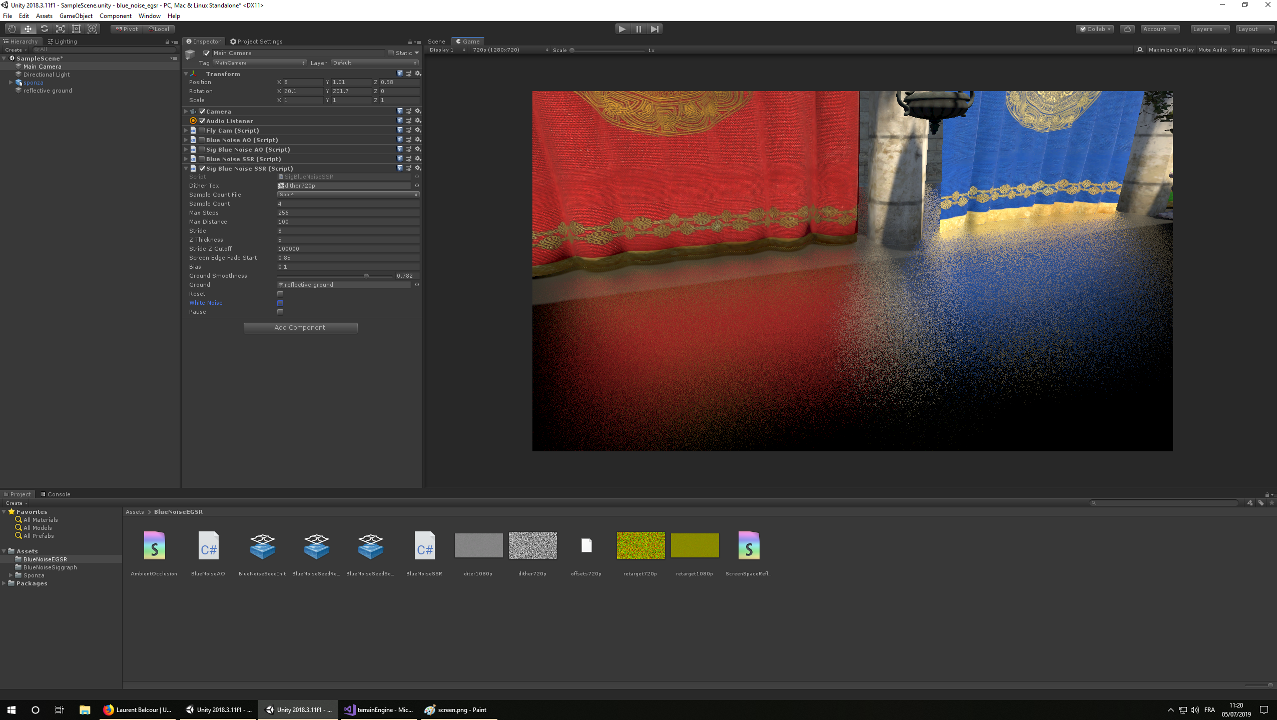
Results: Real-Time Application

In the Unity Engine
- Implementation by Thomas Deliot
- Dithering Ambient Occlusion
- Dithering Screen-Space Reflections

Performances on desktop

Nvidia 2080 GPU at 720p

	White-noise	Ours
AO	0.26 ms	0.54 ms
SSR	2.81 ms	3.06 ms

Fixed cost : 0.25 ms

Live demo !

Limitations : Another Hit in the Wall?

Share limitations with BNDS !
- Can't handle high-dimensional integrands
- Not robust on complex integrands
Still you should use our method rather than BNDS
- Can only do better, not worse
We felt a bit disapointed
A solution : flip the problem
- Do not focus on the sequence
- See our EGSR paper

[Heitz & Belcour 2019]

Our method is not free from limitation and in fact, we do share some of other limitations of BNDS. For example, our method does not scale well in dimensionality or with high-frequency textured assets.

*click* Yet, we always performs either better or simply not worse than BNDS so you should use our method in your renderer.

*click* As a side story, while working on this project, Eric and I were a bit disapointed by those limitations. So, we started to dig more into this dimensionality issue.

*click* We found out that, by forgetting about the sequence and focusing solely on the pixel values we could build a more robust method for rendering animations that we presented at EGSR this year. I encourage you to look at it, all the material is available online.

Summary

A novel progressive screen-space sampler
- That distributes error as a blue-noise
- State-of-the-art convergence
- Efficient and compatible with real-time
Our contributions
- New optimization space: test integrands
- Two stage optimization: ranking and scrambling
Clearing misconceptions
- No more Cranley Patterson rotations
- Blue-noise not restricted to previz.
- Only scratched the surface (see EGSR talk)

To summarize, I presented our new progressive screen-space sampler that aims to distribute the error of Monte-Carlo rendering as a blue-noise in screen-space. Our sampler has state-of-the-art convergence, it is lean and efficient.

*click* To achieve this, we reformulated the optimization of nD dither masks as the optimization of test integrands across pixels of two textures. One that scrambles the samples value and one that reorders the samples order.

*click* The goal of this presentation was not only to introduce you this method, but also to clear some misconceptions. *click* I hope that after this presentation, you will keep away from Cranley-Patterson rotation (unless you know what you are doing). *click* I also hope that I cleared the misconception that blue-noise distribution of the error was only good for previsualization and low sampling counts. It matters as much or even more when doing denoising.

*click* Finally, this talk is also a call for action. We think that we only scratched the surface of what is possible and were surprized to see so few paper on the subject. I hope that this talk will inspire you or others to come up with better solutions.

Thank you for your attention

paper

supp. mat.

code

available at belcour.github.io/blog

A Low-Discrepancy Sampler that Distributes Monte Carlo Errors as a Blue Noise in Screen Space

A screen-space sampler ? 🤨

Our goal

Blue-Noise Dithered Sampling

Blue-Noise Dithered Sampling

Blue-Noise Dithered Sampling

Problem solved ?

Issue #1 : CPR Considered Harmful

Issue #1 : CPR Considered Harmful

Solution #1 : XOR Scrambling

Issue #2 : Lack of Progressivity

Issue #2 : Lack of Progressivity

Issue #2 : Lack of Progressivity

Solution #2 : Change the Optimization Space

Our Method : Test Integrands

Our Method : Test Integrands

Our Method : Test Integrands

Our Method : Sorting

Our Method : Sorting

Summary

Results: Offline Rendering

Results: Real-Time Application

Limitations : Another Hit in the Wall?

Summary

Thank you for your attention

A Low-Discrepancy Sampler that Distributes Monte Carlo Errors
as a Blue Noise in Screen Space

A screen-space sampler ?
🤨