paper  bib  code  slides

Project Summary Many applications in rendering rely on integrating functions over spherical polygons. We present a new numerical solution for computing the integral of spherical harmonics (SH) expansions clipped to polygonal domains. For example the appearance of a surface lit by a polygonal light source is defined as the integral of an hemispherical function, the Bidirectional Reflectance Distribution Function (BRDF), over the projected footprint of the light. Mathematically, we need to compute the integral of this hemispherical function in footprint of the polygon projected on the hemisphere.

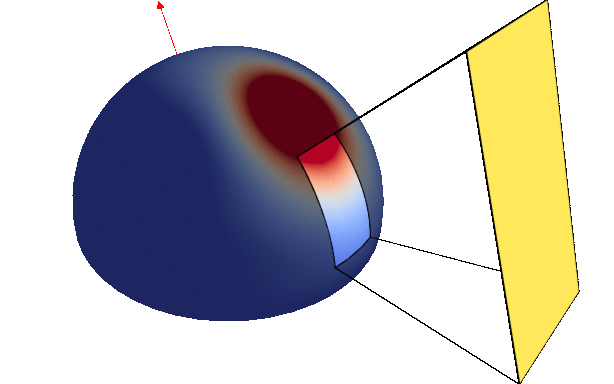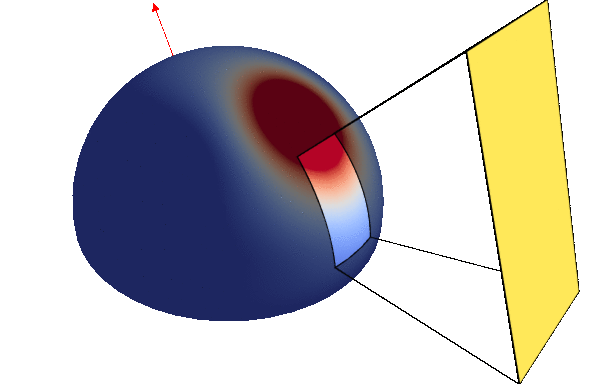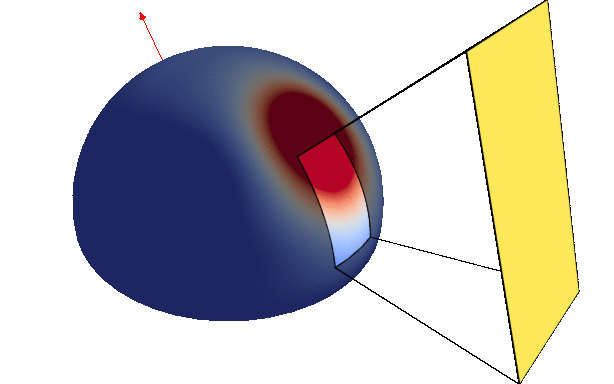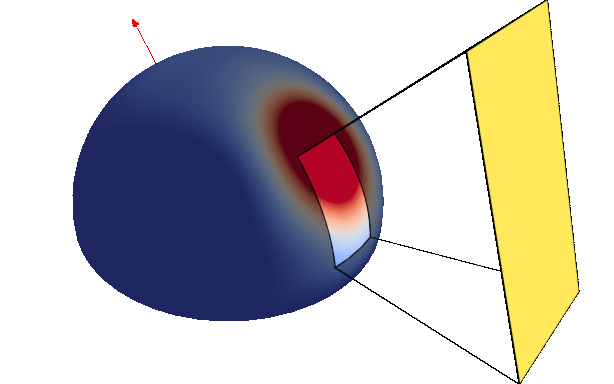Measured BRDF	Integrating over area light

However, such integral is usually not easy to do. We introduce an efficient way to compute the integral of Spherical Harmonics expansion. That is spherical function defined as the weighted sum of Spherical Harmonics (SH).

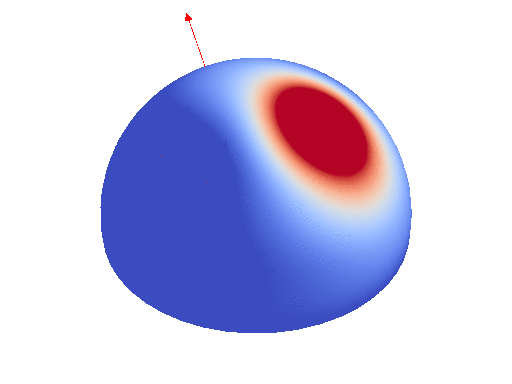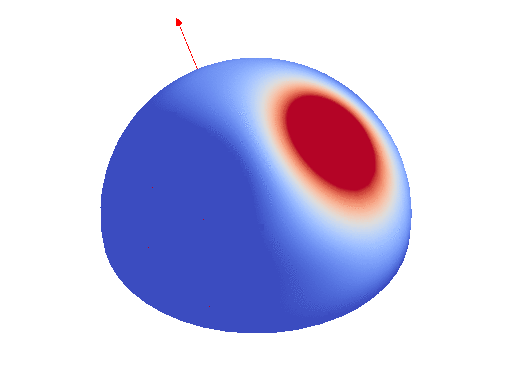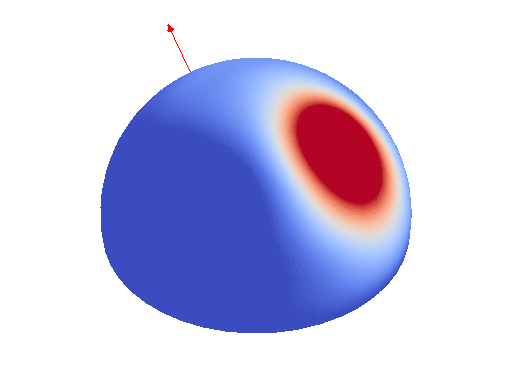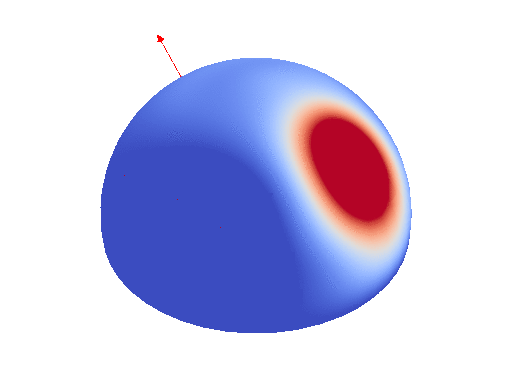
First elements of the SH basis

Any spherical function can be decomposed in an infinite SH expansion. For computation reasons, we restrict ourselves to band-limited expansion, that is expansion with a finite sum. In such as case, we can evaluate the integral of the SH expansion over a polygonal footprint by decomposing each element of the SH basis into a weighted sum of cosine power. Cosine power are spherical function defined using the dot product with a unit direction raised to a power.

Three cosine power directions

We can use Arvo’s method (pdf) to evaluate the integral of each cosine power. We further improve the efficiency of this method by sharing directions in the cosine power basis and using intermediate computation of Arvo’s method.

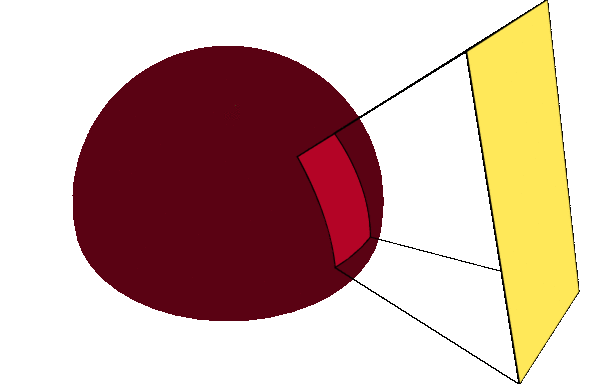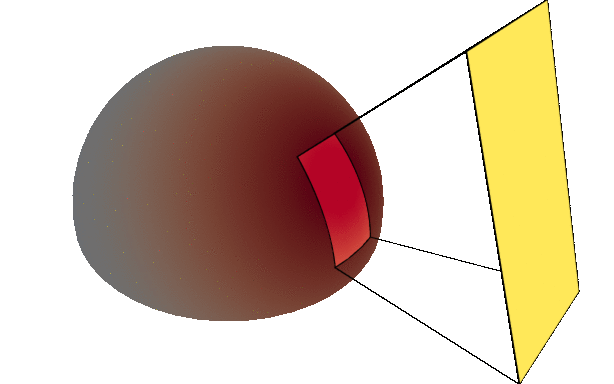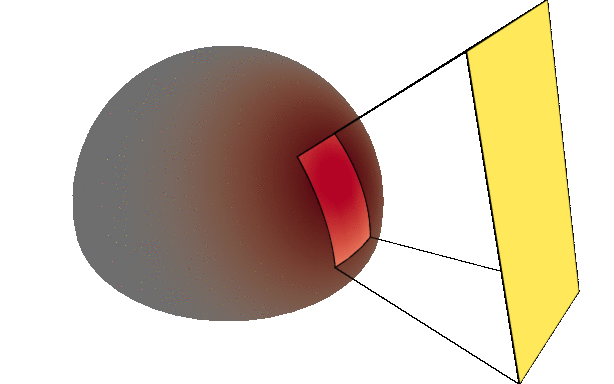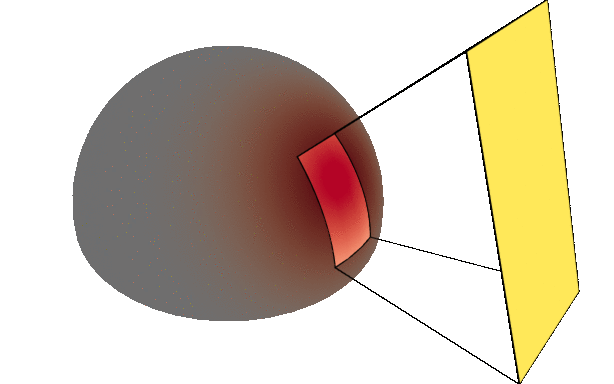
Integrating cosine powers

We apply our technique to problems in rendering, including surface and volume shading, hierarchical product importance sampling, and fast basis projection for interactive rendering. Moreover, we show how to handle general, non-polynomial integrands in a Monte Carlo setting using control variates. Our technique computes the integral of band-limited spherical functions with performance competitive to (or faster than) more general numerical integration methods for a broad class of problems, both in off-line and interactive rendering contexts.